HTML+CSS40 CSS matrix函数

发表于 分类于 阅读次数：

matrix()是CSS的transform的一个基础属性，用它可以实现很多高级、复杂的效果，实际上transfrom的translate、rotate等都是在matrix的基础上实现的简化版的语法。

线性代数基础

了解和使用必须熟悉线性代数的向量和矩阵知识，当初学习的线性代数的课程早就还给老师了，因为不知道有什么用，如果知道今天会用到，当初一定会好好学习线性代数、高数等课程。

（1）向量

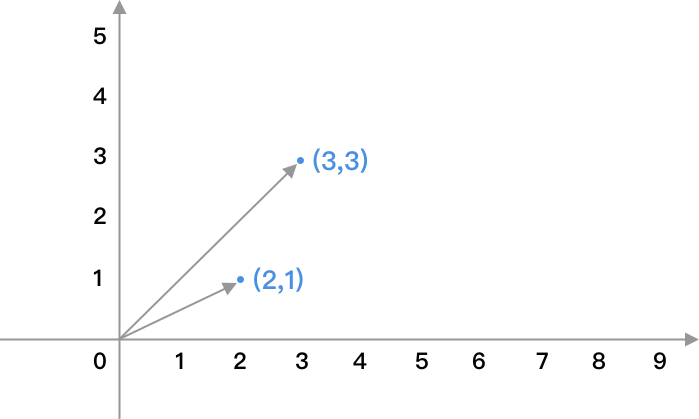
向量用来描述方向和大小，一般使用笛卡尔坐标系来进行向量的描述，比如向量(2, 1)和(3, 3)在坐标系中表示如下：

向量的加法、减法和乘法都是将对应位置的坐标进行运算：

1
2
3
4
5
(8, 2) + (2, 6) = (8 + 2, 2 + 6) = (10, 8)

(8, 2) - (2, 6) = (8 - 2, 2 - 6) = (6, -4)

(8, 2) * (2, 6) = (8 * 2, 2 * 6) = (16, 12)

（2）矩阵

矩阵是高等代数学中的常见工具，将数字按照长方阵列进行排列，便于进行统计分析等高等数学运算，一个2 X 3的矩阵就是说这个矩阵有2行3列

当相同规模的矩阵之间进行相加时，是对应的位置两两相加：

矩阵相乘时，会将前一个矩阵每行对应的位置与后一个矩阵每行对应位置分别相乘，然后将结果相加，得到的矩阵的行数等于左边矩阵的行数，列数等于右边矩阵的列数，例如

matrix方法

CSS3中的transfrom的matrix()方法写法如下：

1
transform: matrix(a,b,c,d,e,f);

一共有六个参数，它对应了一个3*3的矩阵，书写方向是竖向的：

在进行坐标变换时（2D坐标），假设目标点的坐标为(x, y)，那么转换公式如下：

得到的新的矩阵的第一行和第二行就是转换后的横纵坐标。

要注意的是transfrom-origin这个属性是变形的原点，它会影响到点的坐标的计算，我们一帮都会将它设置为0 0

例子

假设有这样一个元素，CSS属性如下：

1
2
3
4
5
6
7
#transformedObject {
  position: absolute;
  left: 0px;
  top: 0px;
  width: 200px;
  height: 80px;
}

此时页面效果如下：

我们对这个元素进行transform: matrix()的变换：

1
2
3
4
5
6
7
8
9
#transformedObject {
  position: absolute;
  left: 0px;
  top: 0px;
  width: 200px;
  height: 80px;
  transform: matrix(0.9, -0.05, -0.375, 1.375, 220, 20);
  transform-origin: 0 0;
}

注意我们设置了transform-origin

进行matrix运算的原则就和上面提到的一样，以(200, 80)的运算过程为例：

应用变换后的效果如下：

matrix与其他属性的关系

matrix是最基本的变化，它有六个参数，这六个参数给定特殊的值，就可以实现translate/rotate等特殊的效果：

以translate距离，当坐标点为(10px, 10px)，进行translate(50px 50px)的变化时，结果的坐标会是(60px, 60px)

如果使用matrix()进行变化，按照上图，需要给出的参数就是matrix(1, 0, 0, 1, 50, 50)，进行运算的过程：

1
2
3
1 0 50     10     1 * 10 + 0 * 10 + 50 * 1     60
0 1 50  *  10  =  0 * 10 + 1 * 10 + 50 * 1  =  60
0 0 1      1      0 * 10 + 0 * 10 + 1  * 1     1

结果是相同的。

对matrix有了了解之后，也就可以使用matrix同时进行复杂的、复合的变化，从而能够实现更复杂的动画。

参考