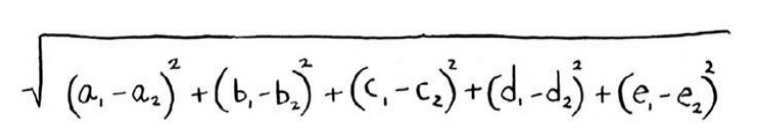《算法图解》读书笔记

发表于 分类于 阅读次数：

《算法图解》读书笔记。

第一章 算法简介

二分查找

二分查找是一种算法，其输入必须是有序的元素列表。

对于包含n个元素的列表，使用二分查找最多需要$\log_2^n$步

对数运算是幂运算的逆运算

1
log_2^n = a  →  2^a=n

在使用大O表示法讨论运行时间时，$\log$指的都是$\log_2$（以2为底）

二分法的JS实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 二分法查找
const binarySearch = (list, target) => {
  let min = 0;
  let max = list.length - 1;
  while (min <= max) {
    const middle = Math.floor((min + max) / 2);
    if (list[middle] > target) {
      max = middle - 1;
    } else if (list[middle] < target) {
      min = middle + 1
    } else {
      return middle;
    }
  }
  return null
};

console.log(binarySearch([1, 3, 5, 7, 9], 3));

对于Python，如果取非整数索引，会自动向下取整，但是JS中不会，因为JS中的数组本质上是一个对象：

1
2
3
4
5
6
7
8
let a = ['x', 'y'];

// 等同于
{
  0: 'x',
  1: 'y',
  length: 2
}

所以如果为JS数组的非整数索引赋值，结果如下：

1
2
3
4
5
let a = [1, 2];
a[2.5] = 100;

console.log(a);
// [1, 2, 2.5: 100]

运行时间

线性时间：最多需要查找的次数与列表长度相同$O(n)$

对数时间：最多需要查找的次数要$\log_2^n$, $O(\log n)$

$O(\log n)$比$O(n)$快，当需要搜索的元素越多，前者比后者快得就越多

大O表示法

仅仅知道算法需要多长时间能运行完还不够，还需要知道运行时间如何随列表增长而增加。大O表示法表示的是算法运行时间的增速。

大O表示法指出的是最糟糕的情况下的运行时间。

一些常见的大O运行时间有：

  • $O(\log n)$，对数时间，例如二分查找
  • $O(n)$，线性时间，例如简单查找
  • $O(n * \log n)$，例如快速排序，一种比较快的排序算法
  • $O(n^2)$，例如选择排序，一种比较慢的排序算法
  • $O(n!)$，例如旅行商问题的解决方案，一种非常慢的算法

image

算法的速度指的并非时间，而是操作数的增速（随着输入的增加，运行时间将以什么样的速度增加）。

第二章 选择排序

内存的工作原理

需要将数据存储到内存是，你请求计算机提供存储空间，计算机给你一个存储地址。需要存储多项数据时，有两种基本方式：数组和链表

数组

数组所分配的内存空间都是紧紧相连的。如果为数组添加新元素时，当前数组占用的内存满了，则需要将数组元素转移到其他地方。可以预留内存，但是都会带来两个缺点：

  1. 浪费内存
  2. 预留的内存用完后，还需要转移元素

数组的优点：需要随机的读取元素时，数组效率很高。

链表

链表中的每个元素都存储了下一个元素的地址，从而使一系列随机的内存地址串在了一起。

链表的优势在与插入元素方面，而且如果需要同时读取所有元素时，链表的效率很高。

在中间插入元素

使用链表插入元素很简单，只需要修改它前面的额按个元素指向的地址。使用数组插入元素时，则必须将后面的所有元素都后移。

在中间插入元素，链表是更好的选择。

删除元素

需要删除元素，链表也是更好的选择。

数组和链表的比较

数组用的更多，因为它支持随机访问，所以数组的读取速度更快。而链表只能顺序访问。

数组和链表常见的操作的运行时间：

– 数组 链表
读取 $O(1)$ $O(n)$
插入 $O(n)$ $O(1)$
删除 $O(n)$ $O(1)$

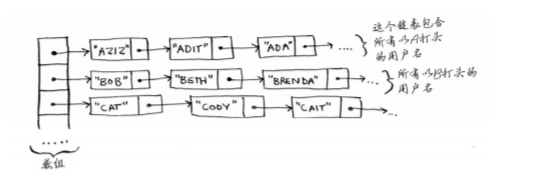
Facebook存储用户信息的方法

Facebook存储用户信息时用的是链表数组，数组包含26个元素，每个元素指向一个链表。

image

插入元素时，对数组的移动最多26次，然后再从它指向的链表中进行插入。

读取元素时，可以直接找到数组中的对应元素，然后在链表中查找。

那么查找元素时，会不会效率太低？

选择排序

选择排序的原理就是每一轮在n个元素中进行查找，找出最小元素，放到结果当中。

每一轮的操作时间复杂度为$O(n)$，这样的操作需要执行n次，所以时间复杂度为$O(n^2)$

有一个问题，每一轮进行后，下一轮要检查的元素会逐渐减少，实际随后检查的元素格式是一个公差为1的等差数列n-1、n-2…2、1，平均每次检查的元素是n/2，因此运行时间为$O(n * n/2)$，但是大O表示法会忽略诸如1/2这样的常数，所以为$O(n^2)$

选择排序的JS实现：（从小到大排序）

1
2
3
4
5
6
7
8
9
10
11
12
function chooseSort (arr) {
  for (let i = 0; i < arr.length; i++) {
    let minIndex = i;
    for (let j = i; j < arr.length; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j
      }
    }
    [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
  }
  return arr;
}

选择排序的速度不是很快，快速排序的速度更快，时间复杂度为$O(n * \log n)$

第三章 递归

递归是一种很多算法都使用的一种编程方法。

递归只是让解决方案更加清晰，并没有性能上的优势。实际上在有些情况下使用循环的性能更好。

基线条件和递归条件

编写递归函数时，必须告诉它何时停止。每个递归函数都有两部分：基线条件（base case）和递归条件（recursive case）。递归条件指的是函数调用自己，而基线条件值得是函数不再调用自己，避免造成无限循环。

栈

栈是一种简单的数据结构，有两种操作：压入和弹出。

计算机内部使用被称为调用栈的栈。在调用过程中，调用另一个函数时，当前函数暂停并处于未完成状态。该函数的所有变量的值都保留在内存中。

在递归调用栈中，包含着未完成的函数调用，自己无需跟踪哪些函数还没有被执行，栈会完成这个步骤。

使用栈很方便，但是也有性能代价，存储详尽的信息可能占用大量的内存。每个函数调用都要占用一定的内存，如果栈很高，那么以为这计算机储存了大量函数调用的信息。

解决方法：

  1. 改用循环
  2. 使用尾递归（尾递归的实现需要确保最后一步只调用自身。做到这一点的方法，就是把所有用到的内部变量改写成函数的参数）

第四章 快速排序

分治法

分治法是解决问题的一种思路，一种递归式问题解决方法。

用分治法解决问题有包括两个步骤：

  1. 找出基线条件（即递归终止的条件），这种条件必须尽可能简单
  2. 不断将问题分解（或者说缩小规模），直到符合基线条件

一道题目：将一个长度为length、宽度为width的矩形均匀地分成方块，并确保分出的方块是最大的

分析这道题，首先要找出递归条件，最容易处理的情况是一条边的长度是另一条边的整数倍。这个时候就可以将矩形均匀地分成方块。

然后找出递归条件，每次递归都需要缩小问题规模。首先找出这块地可容纳的最大方块A，剩余的土地为B，根据欧几里得算法，适用于这小块地的最大方块，也是适用于整块地的最大的方块（就这个算法我就不知道，真做的时候就做出不来）。据此就可以不断的缩小规模，直到满足基线条件：

1
2
3
4
5
6
7
8
9
10
11
12
13
// 找到一个矩形可以均匀的划分的最大的小方块的尺寸
const getMaxSquare = (length, width) => {
  if (width > length) {
    [width, length] = [length, width]
  }
  if (length % width === 0) {
    return width
  }
  if (length === width) {
    return length;
  }
  return getMaxSquare(width, length - width)
};

tips: 编写设计数组的递归函数时，基线条件通常是数组为空或者只包含一个元素。

快速排序

快速排序的思想就是分治法，首先从最简单情况开始分析，找出基线条件，那就是数组为空或者只包含一个元素，然后逐渐增加到两个元素，三个元素。

到了三个元素的时候，首先选出基准值，然后分别找出比基准值小和比基准值大的元素（即分区），这样就得到了三个部分：

  1. 小于基准值的数字组成的数组（无序）
  2. 基准值
  3. 大于基准值组成的数组（无序）

然后对1和3再次进行快速排序，直到满足基线条件（即数组的长度为0或者1）为止。

1
2
3
4
5
6
7
8
9
10
11
12
const quickSort = (arr) => {
  if (arr.length < 1) {
    return arr
  }
  const middleIndex = Math.floor(arr.length / 2);
  const middle = arr.splice(middleIndex, 1)[0];
  const left = [], right = [];
  for(let i = 0; i< arr.length; i++) {
    (middle > arr[i] ? left : right).push(arr[i])
  }
  return quickSort(left).concat(middle, quickSort(right))
};

快速排序的时间复杂度是$O(n * \log n)$

再谈大$O$表示法

c是算法所需要的固定时间量，被称为常量。通常不考虑这个常量，因为如果算法的大$O$运行时间不同，这种常量将无关紧要。

但有时候，常量的影响可能很大，如果运行时间都是$O(n * \log n)$，那么常量就会影响很大。这也是快速排序比合并排序快的原因。

下面要分析一下，快速排序的时间复杂度为什么是$O(n * \log n)$

快速排序的性能高度依赖于选择基准值，如果总是将第一个元素用作基准值，栈长为n（即总共要调用n次），每一轮要比较n个数字，每轮完成时间为$O(n)$，这就是最糟情况，这时候快速排序的运行时间是$O(n^2)$

如果总是将中间的元素用作基准值，栈长变成了$O(\log n)$，每一轮仍然要比较n个数字，每轮完成时间为$O(n)$，这就是最佳情况，这时候快速排序的运行时间是$O(n * \log n)$

要注意的是，最佳情况也是平均情况。只要每次都随机地选择一个数组元素作为基准值，快速排序的平均运行时间也就是$O(n * \log n)$。

快速排序是最快的排序算法之一，也是分治法的典范。

第五章 散列表

散列函数

散列函数是这样的函数，无论输入什么数据，都还给一个数字，即将输入映射到数字，散列函数必须满足：

  1. 每次输出的一致性
  2. 将不同的输入映射到不同的数字

可以使用散列函数来确定元素的存储位置。

散列函数对于散列表的性能至关终于，良好的散列函数让数组中的值呈均匀分布，SHA函数可以用作散列函数。

散列表

使用散列函数和数组，就可以创建一种被称为散列表（hash table）的数据结构。

散列表也被称为散列映射、映射、字典和关联数组。适合用于：

  • 模拟映射关系
  • 防止重复
  • 缓存、记住数据

JavaScript中的对象结构就是语言实现了的散列表结构。

性能

散列表的性能：

– 平均情况 最糟情况
查找 $O(1)$ $O(n)$
插入 $O(1)$ $O(n)$
删除 $O(1)$ $O(n)$

在平均情况下下，散列表执行各种操作的时间都是$O(1)$。$O(1)$被称为常量时间，它并不意味着马上，而是说不管散列表大多，所需的时间与长度无关，都是相同的数值。

所以在JavaScript中，使用对象存储数据并进行查找的性能大于使用数组存储，可以认为是$O(1)$

第六章 广度优先搜索（BFS)

图算法

广度优先搜索算法（breadth-first search，BFS）是一种图算法，可以找出两样东西之间最短的距离，即解决最短路径问题。

解决最短路径问题有两个步骤：

  1. 使用图来建立问题模型
  2. 使用广度优先搜索解决问题

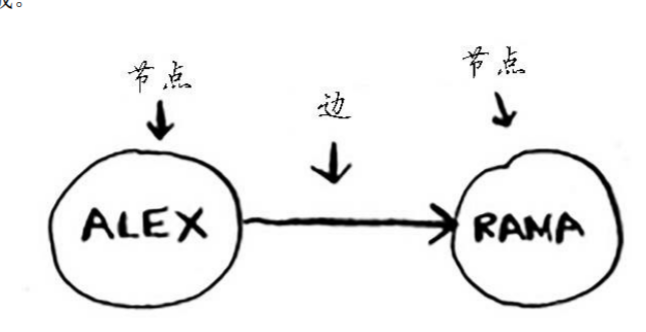
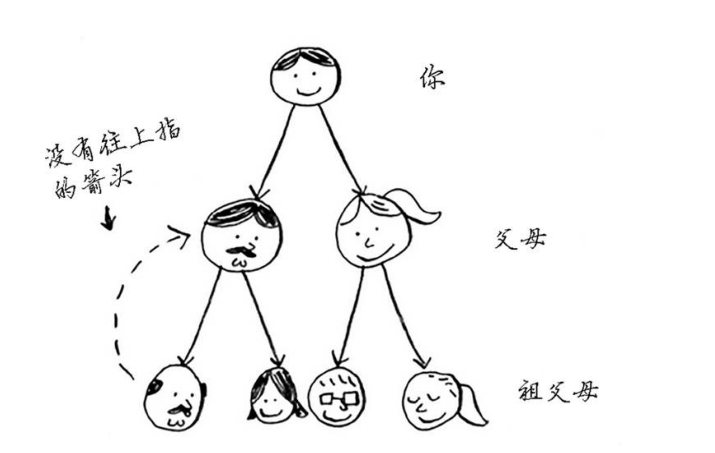
图用来模拟不同的东西是如何连接的，由节点和边构成

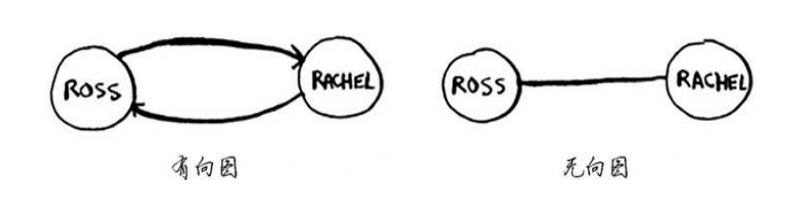
有向图的关系是单向的，边是箭头，箭头指定了关系的方向；无向图没有剪头，关系是双向的。

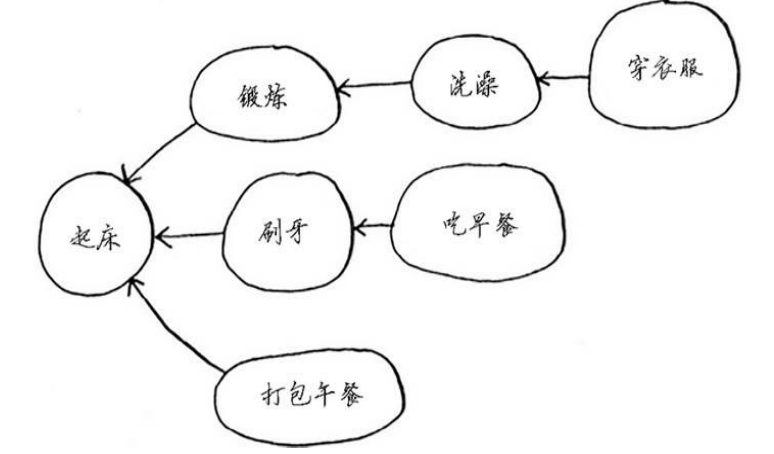
如果任务A依赖于任务B，在列表中任务A就必须在任务B后面，这被称为拓扑排序。

树是一种特殊的图，其中没有往后指的边。

广度优先搜索

广度优先搜索是一种用于图的查找算法，可以解决两类问题：

  1. 从节点A出发，有前往节点B的路径吗
  2. 从节点A出发，前往节点B的哪条路径最短

在广度优先搜索的执行过程中，搜索范围从起点开始逐渐向外延伸，即先检查一度关系，再检查二度关系。广度优先搜索不仅查找从A到B的路径，而且找到的是最短的路径，但是一定要按添加顺序检查，队列（queue）是一种可以实现这种目的的数据结构。

队列

队列只支持两种操作：入队和出队。队列是一种先进先出（First In First Out）的数据结构，而栈是一种后进先出（Last In Frist Out）的数据结构。

实现算法

实现广度优先搜索的关键是，要使用队列来存放要搜索的结果，这个队列是在搜索的过程中不断变增加的。在遍历一层时，如果不是目标，则将这个元素的后代加入到待搜索队列中。同时使用一个对象标记对象是否已经遍历过（针对无向图，防止无限循环出现，对于树结构来说则不需要）

如果是实现最短路径，在将后代元素加入到待搜索队列中时，应该以对象的形式加入，因为要补充一个队列，用来存放当前遍历的路径。

运行时间

在整个关系网中进行搜索，以图算法来看，运行时间至少为$O(边数)$，此外还使用了一个队列来存放待搜索元素，将一个元素添加到队列的时间是固定的为$O(1)$，对每个元素都这样做的总时间为$O(n)$。

所以广度优先搜索的运行时间为$O(边数+顶点数)$，通常写作$O(V+E)$，V是顶点数，E是边数。

第七章 迪克斯特拉算法

广度优先搜索找出的是段数最少的路径，如果每段路径有着不同的权重，要找出最快的路径，可以使用迪克斯特拉算法

使用迪克斯特拉算法

迪克斯特拉算法包含四个步骤

  1. 找出“最便宜”的节点，即可在最短时间内到达的节点
  2. 更新该节点的邻居的开销
  3. 重复这个过程，直到对图中每个节点都这样做了
  4. 计算最终路径

迪克斯特拉算法背后的关键理念：找出图中最便宜的节点，确保没有到该节点的更便宜的路径

负权边

如果有负权边，就不能使用迪克斯特拉算法。

因为节点一旦被处理，就以为这没有前往该节点的更便宜的路径，但是如果有负权边，那么就会在最片的路径被发现后，在负权边的路径上发现更便宜的节点。

在有负权边的图中，要找出最短路径，可以使用贝尔曼-福德算法。

迪克斯特拉算法的实现

迪克斯特拉算法的实现需要四个散列表：

  1. 用于存储节点、节点的邻居以及前往节点邻居的开销graph
  2. 用于存储每个节点的最短开销costs
  3. 用于存储每个节点最短开销情况下的父节点parents
  4. 用于存储已经遍历过的节点processed

实际上上面这四个散列表就是迪克斯特拉算法需要的数据结构，需要将图转换为对应的数据结构后，对这种特定的数据结构使用算法，达到目的。

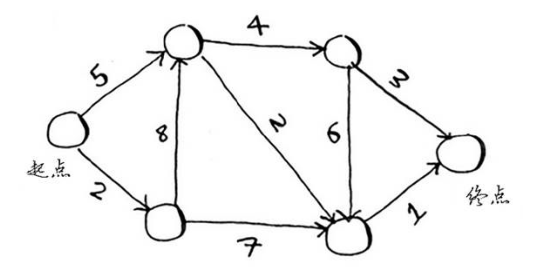
以下面的图距离：

首先实现第一个散列表（也就是JS中的对象）graph

1
2
3
4
5
6
7
8
// 用于存储节点、节点的邻居以及前往节点邻居的开销
const graph = {
  start: {a: 5, b: 2},
  a: {c: 4, d: 2},
  b: {a: 8, d: 7},
  c: {d: 6, end: 3},
  d: {end: 1},
};

然后实现第二个对象costs：

1
2
3
4
5
6
7
8
// 用于存储每个节点的最短开销
const costs =  {
  a: 5,
  b: 2,
  c: Infinity,
  d: Infinity,
  end: Infinity,
};

其中，没有计算的节点的开销用了Infinity无穷大来表示。

然后实现第三个对象parents

1
2
3
4
5
6
7
8
// 用于存储每个节点最短开销情况下的父节点
const parents = {
  a: 'start',
  b: 'start',
  c: '',
  d: '',
  end:'',
};

第四个对象可以在函数内部声明一个对象实现，也可以直接改造第二个对象，添加一个是否遍历的属性。

构造数据结构完成之后，来实现dijkstra算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
// 找到开销最小的，并且没有遍历过的节点
const findLowestCostNode = (costs, processed) => {
  // 筛选出没有遍历过的节点
  const unProcessed = Object.keys(costs).filter(key => !processed[key]);
  // 如果存在没有遍历过的节点
  if (unProcessed && unProcessed.length > 0) {
    // 找出开销最小的节点
    return unProcessed.sort((a, b) => costs[a] - costs[b])[0]
  }
  // 不存在没有遍历过的节点时
  return null;
};

// 生成加权图中的最短路径
const getFullPath = parents => {
  let key = 'end';
  let path = [];
  while (key !== 'start') {
    path.unshift(key);
    key = parents[key];
  }
  path.unshift('start');
  return path.join('→')
};

// 迪科特斯拉算法
const dijkstra = (graph, costs, parents) => {
  // 记录所有遍历过的节点
  let processed = {};
  // 找到开销最小的，并且没有遍历过的节点
  let node = findLowestCostNode(costs, processed);
  // while 循环在所有节点都遍历过后结束
  while (node) {
    // 找到当前节点的所有相邻节点
    let neighbors = graph[node];
    // 找到到达当前节点的开销
    let cost = costs[node];
    // 对所有相邻节点进行遍历
    for (const neighborNode in neighbors) {
      // for...in 的安全性检查
      if (neighbors.hasOwnProperty(neighborNode)) {
        // 找出新的到达相邻节点的开销
        const newCost = cost + neighbors[neighborNode];
        // 如果计算出的新的开销小于已记录的开销，则进行更新
        if (newCost < costs[neighborNode]) {
          // 更新开销
          costs[neighborNode] = newCost;
          // 更新父节点
          parents[neighborNode] = node;
        }
      }
    }
    // 将当前节点标记为已经处理过
    processed[node] = true;
    // 找出接下来要处理的节点，并循环，直到所有节点都被处理过
    node = findLowestCostNode(costs, processed);
  }
  // 返回最终的开销和路径
  return {
    cost: costs['end'],
    path: getFullPath(parents),
  }
};

计算结果：

1
{ cost: 8, path: 'start→a→d→end' }

第八章 贪婪算法

教室调度问题

教室调度问题可以采用贪婪算法，具体做法如下：

  1. 选出最早结束的课
  2. 选择第一堂课结束后的，并且结束最早的课
  3. 重复上面的步骤

贪婪算法很简单：每一步都采取最优的做法。每步都选择局部最优解，最终得到的就是全局最优解。

背包问题

对于背包问题，贪婪算法显然不能获得最优解。些时只需要找到一个能够大致解决问题的算法，此时贪婪算法刚好可以派上用场，因为它们实现起来很容易，得到的结果由于正确结果相当接近。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 贪婪算法求解背包问题近似解
const knapsackProblem = () => {
  const bagSize = 4;
  const items = [
    {name: 'sound', size: 4, value: 3000},
    {name: 'laptop', size: 3, value: 2000},
    {name: 'guitar', size: 1, value: 1500},
    {name: 'iphone', size: 1, value: 2000},
  ];

  let value = 0;
  let names = [];
  let remainSize = bagSize;

  // 从价值最大的开始装，能装多少算多少
  items.sort((a, b) => b.value - a.value).forEach(v => {
    if (v.size <= remainSize) {
      value += v.value;
      names.push(v.name);
      remainSize = remainSize - v.size;
    }
  });

  return {
    value, names
  };
};

集合覆盖问题

假设需要将一个广播节目让全美50个州的听众都收听得到，需要在尽可能少的广播台播出，这就是集合覆盖问题。

解决覆盖问题非常难，具体方法如下：

  1. 列出每个可能的广播台的集合，被称为幂集，可能的子集有$O(2^n)$个
  2. 在这些集合中，选出覆盖全部50个州的最小集合

运行时间为$O(2^n)$，需要一种近似算法

近似算法

使用贪婪算法可以得到非常近似的解：

  1. 选出这样一个广播台，它覆盖了最多的未覆盖州（即便这个广播台覆盖了一些已覆盖的州，也没有关系）
  2. 重复第一步，直到覆盖了所有的州

这是一种近似算法，在获得精确解需要的时间太长时，可以使用近似算法。判断近似算法优劣的标准如下：

  1. 速度有多快
  2. 得到的近似解与最优解的接近程度

这个例子的贪婪算法的时间复杂度为$O(n^2)$，其中n是广播台的数量。

这种算法的关键是求出statesNeeded（需要覆盖的州）和stateForStation（电台能够覆盖的州）的交集，求出的就是当前广播电台覆盖的所有还未覆盖的州。

在所有没有选择的电台中进行比那里，找出上面提到的交集最大的电台。不断重复这个过程，直到所有的州都被覆盖为止。

NP完全问题

为了解决集合覆盖问题，你必须计算每个可能的集合，这与旅行商问题相似，需要计算每条可能的路径。

  • 当有1个城市时，可能的路线有1条
  • 当有2个城市时，可能的路由先2条
  • 当有3个城市时，可能的路由先6条
  • 当有4个城市时，可能的路由先24条

规律就是，每增加一个城市，需要计算的路线数都将增加，可以认为增加一个城市，可能的路径就以任何一个城市为起点（n）个，重复前一种情况的可能的路径数，也就是说当有5个城市时，任选一个作为起点，有5种情况，都是「当有4个城市时」的路径树24，也就是24重复了5遍，也就是120条

这是阶乘函数，如果涉及到的城市非常多，根本就无法找出旅行商问题的正确解。

旅行商问题和集合覆盖问题有一些共同之处：需要计算所有的解，并从中选出最小/最短的那一个。这两个问题都属于NP完全问题。

旅行商问题的近似求解：随便选择出发城市，然后选择要去的下一个城市时，都选择还没去的最近的城市。选择的路径可能不是最短的，但是也比较接近了。

如何识别NP完全问题

判断问题是不是NP完全问题很难，易于解决的问题和NP完全问题的差别通常很小。可以通过以下几点来判断NP完全问题：

  • 元素较少时算法的运行速度非常快，但随着元素数量增加，速度会变得非常慢
  • 涉及“所有组合”的问题通常是NP完全问题
  • 不能将问题分成小问题，必须考虑各种可能的情况，这可能是NP完全问题
  • 如果问题涉及序列（如旅行商问题的城市序列）且难以解决，它可能就是NP完全问题
  • 如果问题涉及集合（如广播台集合）且难以解决，它可能就是NP完全问题
  • 如果问题可转换为集合覆盖问题或旅行商问题，那它肯定是NP完全问题

第九章 动态规划

动态规划可以在给定约束条件下找到最优解。在问题可以分解为彼此独立且离散的子问题时，就可以使用动态规划来解决。

为动态规划问题建模时的小窍门：

  • 每种动态规划解决方案都涉及网格
  • 单元格中的值通常就是要优化的值
  • 每个单元格都是一个子问题

在绘制网格时，需要回答如下问题：

  • 单元格中的值是什么
  • 如何将这个问题划分为子问题
  • 网格的坐标轴是什么

要注意，最终答案不一定在最后一个单元格中。

背包问题

背包问题就是典型的动态规划的应用之一。

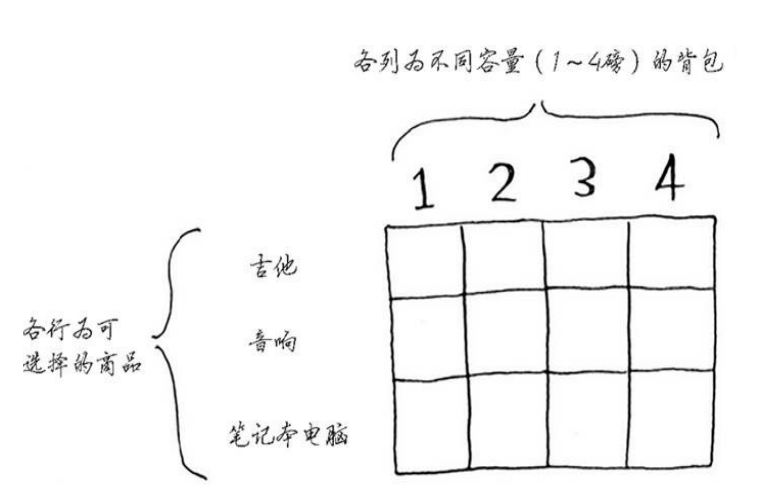
动态规划先解决子问题，在逐步解决大问题。每个动态规划算法都从一个网格开始，背包问题的网格如下：

填充的过程是逐行进行的，原则是保证当前单元格的值为此列的最大值。如果装入当前单元格的物品后，重量有剩余，则回退一行，找到剩余重量对应的最大值。

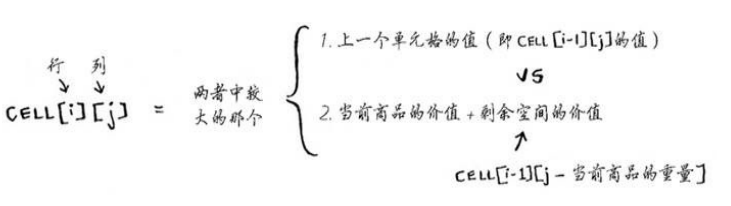
使用的公式为：

通过表格求解子问题，可以合并两个子问题的解来得到更大问题的解。

下面编写代码：

（感觉这个代码是为了这个算法生凑出来的，其实关键点把握住就行了，一是上面的公式，而是通过求解子问题，然后通过合并来求解更大问题）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
const knapsackProblem = () => {
  const bagSize = 4;
  const items = [
    {name: 'sound', size: 4, value: 3000},
    {name: 'laptop', size: 3, value: 2000},
    {name: 'guitar', size: 1, value: 1500},
  ];

  // 存储结果的表格
  const cell = [];

  // 空格子
  class CellClass {
    constructor() {
      this.value = 0;
      this.names = [];
    }
  }

  // 外层遍历物品
  for (let i = 0; i < items.length; i++) {
    // 声明新的一行
    cell[i] = [];
    // 针对的物品
    const item = items[i];
    // 当前商品的价值
    const currentValue = item.value;

    // 内层遍历重量
    for (let j = 0; j <= bagSize; j++) {
      // 当前格子装入物品后的剩余空间
      const remainSize = j - item.size;
      // 上一个单元格
      const lastCell = (cell[i - 1] && cell[i - 1][j]) ? cell[i - 1][j] : new CellClass();
      // 上一个单元格的值（之前的最大值）
      const lastCellValue = lastCell.value;

      // 如果能装下这个物品
      if (remainSize >= 0) {
        // 剩余空间对应的单元格
        const remainCell = (cell[i - 1] && cell[i - 1][remainSize]) ?cell[i - 1][remainSize]: new CellClass();
        // 剩余空间的价值
        const remainValue = remainCell.value;
        // 预期的最大值
        const currentMaxValue = currentValue + remainValue;

        // 如果预期的最大值更大
        if (currentMaxValue > lastCellValue) {
          cell[i][j] = {value: currentMaxValue, names: [item.name, ...remainCell.names]}
        } else {
          cell[i][j] = {value: lastCellValue, names: lastCell.names}
        }
      } else {
        // 装不下这个物品则取上一个单元格
        cell[i][j] = lastCell
      }
    }
  }
  console.log(cell);

  return cell[items.length - 1][bagSize]
};

可以偷商品的一部分吗

偷商品的一部分，不能使用动态规划处理。动态规划只能处理要么拿走整件商品，要么就不拿的情况，没法判断该不该拿走商品的一部分。

这种情况应该使用贪婪算法来处理，首先尽可能多的拿价值高的商品，如果拿光了在尽可能拿价值次高的商品，以此类推。

可以相互依赖吗

如果各个项目之间有依赖情况，那么是没有办法使用动态规划来建模的。

动态规划算法能够解决子问题，并且使用这些答案来解决大问题。但是仅当每个子问题都是离散的，即不依赖于其他子问题时，动态规划才管用。

最长公共子串

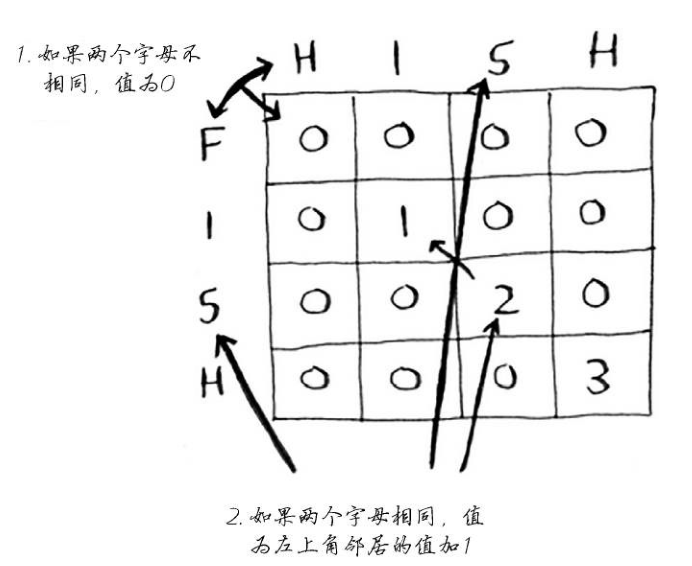
在填充表格时，没有找出计算公式的简单办法，必须通过尝试才能找出有效的公式。有些算法并非精确的解决步骤，而是帮助你理清思路的框架。

在计算FISH和HISH的最大公共子串时，填写出来的表格和计算公式是：

实现的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
const maxSubstring = (string1, string2) => {
  let result = {
    value: 0,
    string: ''
  };
  let cell = [];
  for (let i = 0; i < string1.length; i++) {
    cell[i] = [];
    for (let j = 0; j < string2.length; j++) {
      if (string1[i] === string2[j]) {
        const lastCell = cell[i - 1] && cell[i - 1][j - 1];
        cell[i][j] = {
          value: lastCell ? lastCell.value + 1 : 1,
          string: lastCell ? lastCell.string + string1[i] : string1[i]
        }
      } else {
        cell[i][j] = {value: 0, string: ''};
      }
      if (result.value < cell[i][j].value) {
        result.value = cell[i][j].value;
        result.string = cell[i][j].string;
      }
    }
  }
  return result
};

也可以用这个算法来解决之前遇到过的《前端练习10 连续子串最大和》的问题，具体分析过程看那篇笔记吧。

最长公共子序列

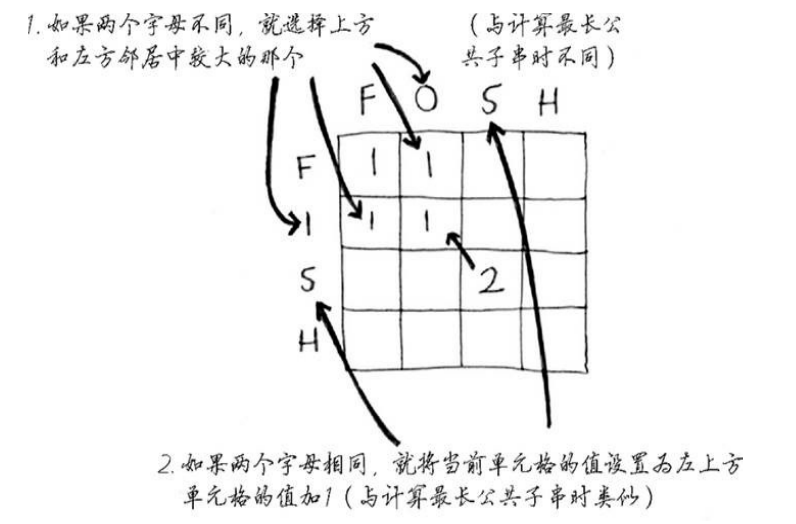
与最长公共子串不同，最长公共子序列不需要是连续的，比如FOSH与FISH的最长公共子串是SH，长度是2，而最长公共子序列是FSH，长度是3

这个问题在计算单元格数据时使用的公式与最长子串不同：

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// 最长公共子序列
const maxSubsequence = (string1, string2) => {
  let result = {
    value: 0,
    string: '',
  };

  const cell = [];

  for (let i = 0; i < string1.length; i++) {
    cell[i] = [];
    for (let j = 0; j < string2.length; j++) {
      if (string1[i] === string2[j]) {
        const lastCell = cell[i - 1] && cell[i - 1][j - 1];
        cell[i][j] = {
          value: lastCell ? (lastCell.value + 1) : 1,
          string: lastCell ? (lastCell.string + string1[i]) : string1[i],
        };
        // 更新结果
        if(cell[i][j].value > result.value) {
          result = cell[i][j]
        }
      } else {
        const lastRowCell = cell[i] && cell[i][j - 1] || { value: 0, string: '',};
        const lastColCell = cell[i - 1] && cell[i - 1][j]|| { value: 0, string: '',};
        if (lastRowCell.value > lastColCell.value) {
          cell[i][j] = {
            value: lastRowCell.value,
            string: lastRowCell.string,
          }
        } else {
          cell[i][j] = {
            value: lastColCell.value,
            string: lastColCell.string,
          }
        }
      }
    }
  }

  return result;
};

小结

  • 需要在给定约束条件下优化某种指标时，动态规划很有用
  • 问题可以分解为离散的子问题时，可以使用动态规划来解决
  • 每种动态规划解决方案都涉及网格
  • 单元格中的值通常是你要优化的值
  • 每个单元格都是一个子问题，需要考虑如何将问题分解为子问题
  • 没有放之四海而皆准的计算动态规划解决方案的公式

第十章 K最近邻算法

K最近邻算法（k-nearest neighbours, KNN）简单的说就是在对一个事物分类时，如果自身没有准确的特征值用来分类，就可以看距离它最近的邻居，借此对目标分类。

创建推荐系统

（1）特征抽取

要比较推荐系统的用户，就需要以某种方式将他们放到图表中，需要将每个用户转换为这一组坐标，然后就可以计算他们的距离了。

特征抽取就是将物品转换为一系列可比较的数字。

一种抽取特征值的方法：

通过这些特征值可以计算距离：

（2）回归

所谓回归，就是使用KNN来做两项基本工作：分类和回归：

  • 分类就是编组
  • 回归就是预测结果（比如一个数字）

比如，找出与目标最接近的5个邻居，求这些人的平均分，就是回归。

可以使用余弦相似度来代替距离公式，能够更准确的找出相似的邻居。

（3）挑选合适的特征值没有通用的准则，必须考虑各种需要考虑的因素

能够挑选合适的特征事关KNN算法的成败。

机器学习

刚才的推荐系统实际上就是一个机器学习的例子，还有其他机器学习的例子

（1）OCR，光学字符识别，要自动识别字符，可以使用KNN

  • 浏览大量的图像，将这些数字的特征提取出来（也就是训练）
  • 遇到新图像时提取该图像的特征，再找出它最近的邻居

大多数及其学习算法都包含训练的步骤，要让计算机完成任务，必须先训练它

（2）垃圾邮件过滤器

垃圾邮件过滤器使用了一种简单算法：朴素贝叶斯分类器，用数据对分类器进行训练后，收到新的邮件，分析邮件中每个单词在垃圾邮件中出现的概率是多少

第十一章 接下来如何做

树

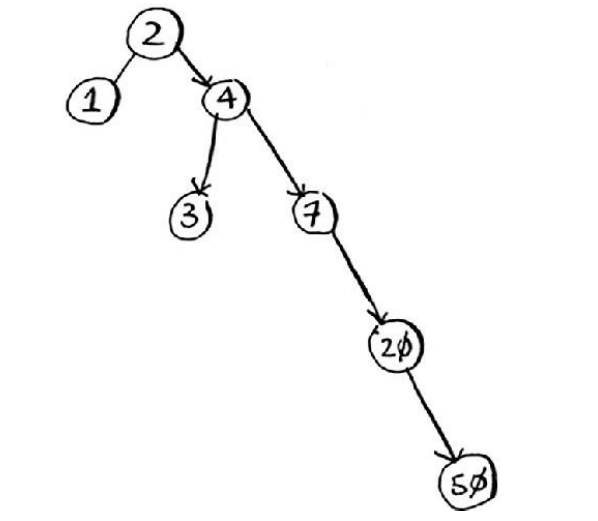
二叉树查找（binary search tree，BST）的特征：

  1. 左子树的所有节点的值都小于或等于它的根节点的值
  2. 右子树上所有节点的值均大于或等于它的根节点的值

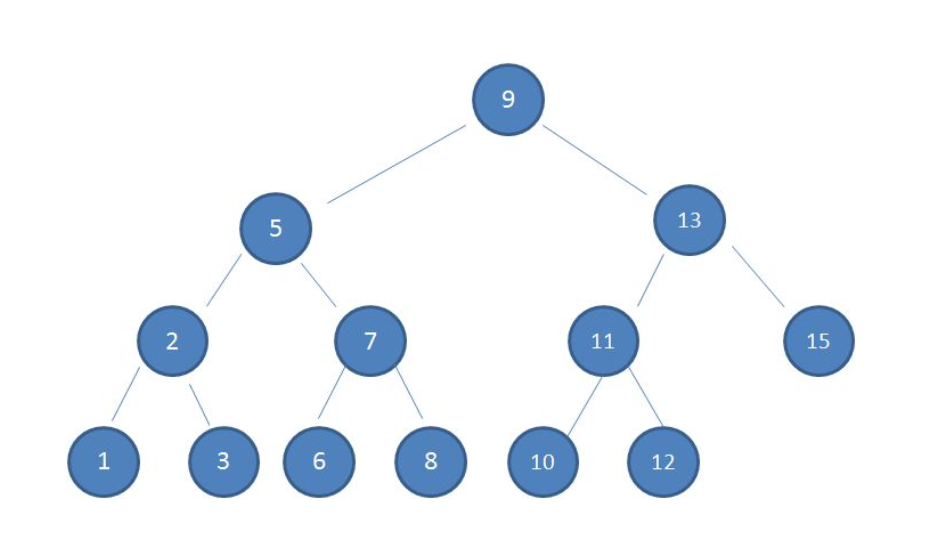
下面就是一棵典型的二叉查找树：

在利用二叉查找树查找节点时的思想就是二分法查找的思想，平均运行时间为$O(\log n)$，最糟的情况下所需的时间为$O(n)$。在有序数组中查找时即便是最糟情况下所需的时间也只有$O(\log n)$，但这不意味着有序数组比二叉查找树更佳，因为二叉查找树的插入和删除操作的速度快的多：

二叉树的查找的最大次数等同于二叉查找树的高度。

二叉查找树也有一些缺点：不能随机访问，并且如果二叉查找树处于失衡状态下，查找的性能会大打折扣，几乎变成了线性查找：

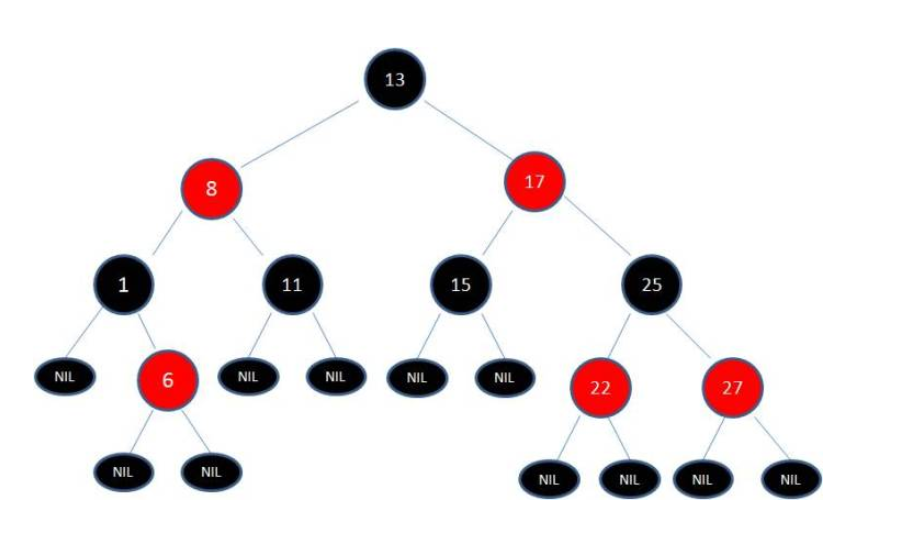
如何解决二叉树多次插入新节点而导致的不平衡呢？可以使用红黑树来解决，红黑树（Red Black Tree）是一种自平衡的二叉查找树，除了符合二叉查找树的基本特征之外，还有一系列的附加特性，通过每次插入新节点后的处理（变色、反转）来保证自身符合红黑树的附加特性，实现了自平衡

知乎这篇文章讲解二叉查找树和红黑树讲的很好，通俗易懂。

反向索引

搜索引擎的工作原理就是使用反向索引这种数据结构：一个散列表，将单词映射到包含它的页面

傅里叶变换

（1）傅立叶级数

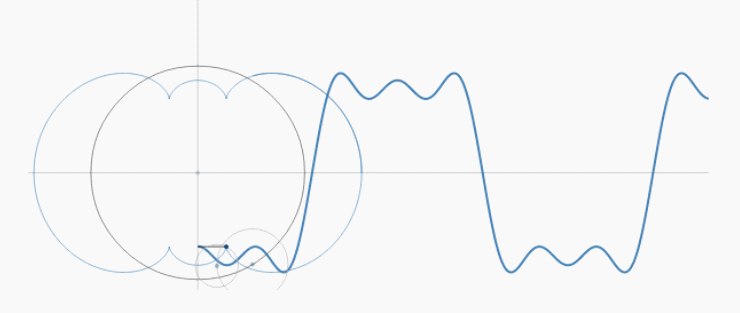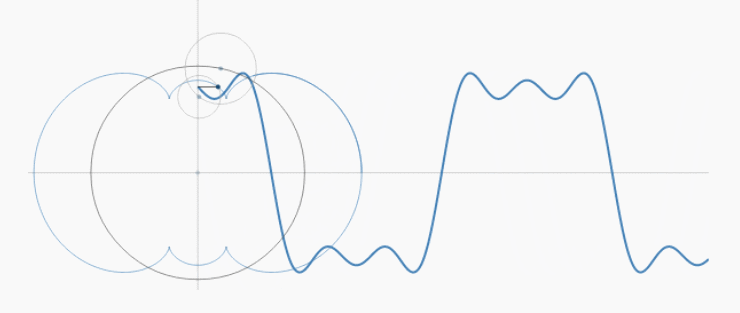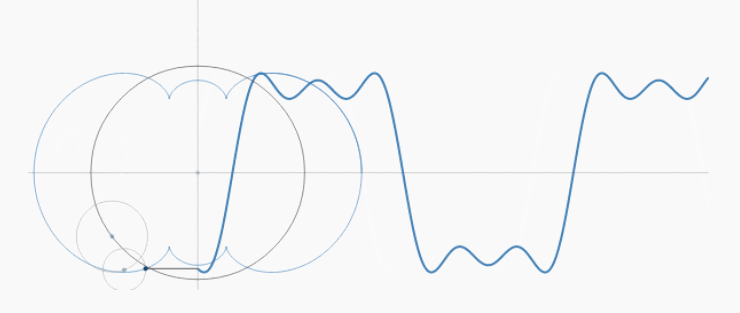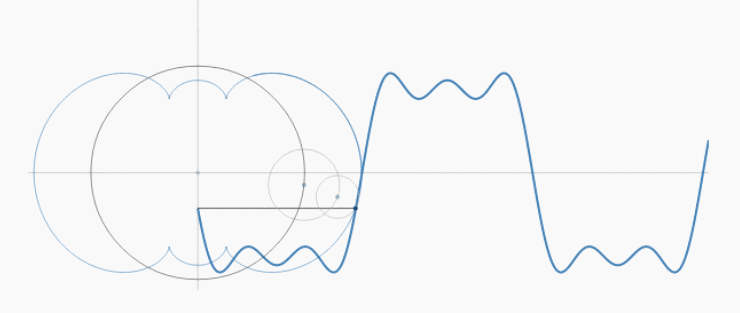
傅立叶级数实际上就是把$f(x)$看作是圆周运动的组合。只是$x$是不断变大的，而不是绕着圆变换的，所以就画出了函数曲线：

不断增大的$x$就好像是时间流逝，永不回头，所以我们也称为“时域”。

时域是现实存在的，频域却是生造的了，理解起来更加抽象。但频域是傅立叶级数（变换）更本质的内容。

傅里叶技术的一个典型应用就是图像压缩，哪些基上的坐标值特别小，就可以丢掉，这样就可以压缩图像，JPG就是利用傅里叶进行图片压缩的

（2）傅里叶变换

傅立叶级数是基于周期函数的，如果将周期推广到$\infty$，那么也就变为了非周期函数，这就是傅里叶变换

这部分的内容可以参考如何通俗地理解傅立叶变换？和如何理解傅立叶级数公式？

MapReduce

MapReduce是一种流行的分布式算法，可以通过流行的开源工具Apache Hadoop来是实现它。

Hadoop是一个由Apache基金会所开发的分布式系统基础架构。用户可以在不了解分布式底层细节的情况下，开发分布式程序。充分利用集群的威力进行高速运算和存储。Hadoop实现了一个分布式文件系统（Hadoop Distributed File System），简称HDFS。HDFS有高容错性的特点，并且设计用来部署在低廉的（low-cost）硬件上；而且它提供高吞吐量（high throughput）来访问应用程序的数据，适合那些有着超大数据集（large data set）的应用程序。HDFS放宽了（relax）POSIX的要求，可以以流的形式访问（streaming access）文件系统中的数据。

Hadoop的框架最核心的设计就是：HDFS和MapReduce。HDFS为海量的数据提供了存储，则MapReduce为海量的数据提供了计算。

分布式算法非常实用用于在短时间内完成海量工作，其中的MapReduce基于两个简单的历年：映射（map）函数和归并（reduce）函数

映射函数很简单，它接受一个数组，并对其中的每个元素执行同样的处理。映射函数是将一个数组转换为另一个数组。而归并函数的理念是将很多项归并为一项，将一个数组转换为一个函数

MapReduce是第一代计算引擎，Tez和Spark是第二代。MapReduce的设计，采用了很简化的计算模型，只有Map和Reduce两个计算过程（中间用Shuffle串联），用这个模型，已经可以处理大数据领域很大一部分问题了。

关于MapReduce的介绍可以看这篇文章。

布隆过滤器和HyperLogLog

布隆过滤器是为了解决在海量数据中查找某个键是否存在的技术，它是一种概率性型数据结构，提供的答案有可能不对，但很可能是正确的。

判断网页以前是否已搜集，可以不适用散列表，而是用布隆过滤器，它的优点在于占用的存储空间少，非常适合于不要求答案绝对准确的情况。

关于布隆过滤器的原理可以参考这篇文章。

HyperLoglog是一种类似于布隆过滤器的算法。可以近似地计算集合中不同的元素数，提供不精确的去重计数，它也不能给出准确的答案，但是八九不离十，而占用的内存空间却少得多。关于HypoerLogLog的解释可以阅读这篇文章。

上面的这两种都是概率算法，都要求允许统计巨量数据面前的误差范围可以接受。

SHA算法

SHA函数（secure hash algorightm）是一种安全散列算（也就是哈希算法），给定一个字符串，SHA返回其散列值。

有两种应用：

（1）比较文件

对于不同的字符串，SHA生成的散列值不同，可以利用SHA来判断两个文件是否相同，在比较超大型文件时很有用，可以计算文件的SHA散列值，再对结果进行比较。

（2）检查密码

SHA能在不知道原始字符串的情况下进行比较，进行密码登陆时，不会直接存储密码，而是比较散列值。网站保存的不是原始密码，而是密码的散列值。

SHA散列算法是单项的，可以根据字符串计算散列值，但是无法根据散列值推出原始字符串。

SHA实际上是一系列散发：SHA-0/SHA-1/SHA-2/SHA-3，SHA-0和SHA-1被发现存在一些缺陷，应该使用SHA-2和SHA-3来计算密码散列值，最安全的散列函数是bcrypt。

关于各种散列算法的介绍可以阅读这篇文章。

局部明暗的散列算法

SHA算法是局部不敏感的，对一个字符串，如果只改动了其中一个字符，得到的两个散列值是完全不同的，这就让攻击者无法通过比较散列值是否类似来破解密码。

如果希望散列函数是局部明暗的，可以使用Simhash，对字符串进行细微的修改，Simhash生成的散列值也只存在细微的差别。这就可以通过比较散列值来比较两个字符串的相似程度，应用：

  • Google来判断网页是否被收集
  • 论文查重/资源查重

需要检查两项内容的相似程度时，可以使用Simhash。

Diffie-Hellman密钥交换

Diffie-Hellman密钥交换解决了两个问题：

  1. 双方无序知道加密算法，不必会面协商使用的加密算法
  2. 破解加密非常困难

使用了两个密钥：公钥和私钥。它的替代者是RSA，被广泛使用。

线性规划

线性规划用于在给定约束条件下最大限度的改善指定的指标。

所有的图算法都可以使用线性规划来实现，图问题知识线性规划的一个子集。

线性规划使用Simplex算法。