前端练习10 连续子串最大和

发表于 2018-12-04 更新于 2019-08-11 分类于前端练习阅读次数：

求连续子串最大和的练习。

题目

输入一组整数，例如：[-23, 17, -7, 11, -2, 1, -34, 2, -21, 9, 12]，求出子序列的最大和

实现1

先尝试一种最暴力的方法，求最大子串，那么就将所有的子串计算出来，然后从中选出最大的

const getMax = arr => {
  let result = [];
  let temp;
  for (let i = 0; i < arr.length; i++) {
    temp = 0;
    for (let j = i; j < arr.length; j++) {
      temp += arr[j];
      result.push(temp)
    }
  }
  return Math.max(...result)
};

实现2

可以对上面的方法进行优化，没有必要将所有的子串都保存起来，在计算过程中就可以实时的比较当前的最大值，最终返回的也是这个最大值

const getMax = arr => {
  console.time('getMax');
  let max = arr[0];
  let temp;
  for (let i = 0; i < arr.length; i++) {
    temp = 0;
    for (let j = i; j < arr.length; j++) {
      temp += arr[j];
      max = Math.max(max, temp)
    }
  }
  return max
};

这种解法的时间复杂度为O(n²)

实现3

实际上这是一道动态规划题目，以我对动态规划浅显的理解，就是从已有的状态中，推测下一状态的最优解。

要计算最优解，我们假设计算到的序列是i，这之前的子串和是temp，同时保存一个临时变量result，将temp和result每一步遍历都进行比较，保证result存的永远是当前结果的最大值。

如果temp小于0，那么就抛弃temp，从i开始重新计算。

这样实际上只保留了计算过程中最近一步的状态

const getMax = arr => {
  console.time('getMax');
  let temp = 0;
  let max = arr[0];
  for (let i = 0; i < arr.length; i++) {
    // 如果前面计算的子串和<0，那么就不要了
    if (temp < 0) {
      temp = 0
    }
    temp += arr[i];
    // 上面可以简化为
    // Math.max(0, tempMax) + arr[i]
    
    max = Math.max(max, temp)
  }
  return max
};

这种解法的时间复杂度为O(n)

今天重新做，优化了一下，感觉更好理解一点（2019.01.25）：

const getMax = arr => {
  let result = 0;
  let temp = 0;
  for (let i = 0; i < arr.length; i++) {
    temp += arr[i];
    if (temp < 0) {
      temp = 0
    }
    // 保证永远是当前结果的最大值
    result = Math.max(temp, result);
  }
  return result
};

实现4

还可以用分治法来解决这个问题，连续最大子序列出现的位置有三种可能：

数组的左半部分MaxL
数组的右半部分MaxR
横跨数组左右两个部分MaxM

我们要做的就是分别求出上面三个值，然后取最大值就可以了，所以有：

1	const reuslt = Max.max(MaxL, MaxR, MaxM)

那么现在的关键就是分别取得这三个值了：

const getMax = (arr, start = 0, end = arr.length - 1) => {
  if (start > end) {
    return 0
  } else if (start === end) {
    return arr[start]
  }
  // 取中间位置
  let middle = Math.floor((start + end) / 2);
  // 求横跨左右的最大连续子序列中左半部分的最大值
  let maxMiddleL = arr[middle];
  let tempL = 0;
  for (let i = middle; i >= start; i--) {
    tempL += arr[i];
    maxMiddleL = Math.max(tempL, maxMiddleL)
  }
  // 求横跨左右的最大连续子序列中右半部分的最大值
  let maxMiddleR = arr[middle + 1];
  let tempR = 0;
  for (let i = middle + 1; i <= end; i++) {
    tempR += arr[i];
    maxMiddleR = Math.max(tempR, maxMiddleR)
  }
  // 获得横跨左右的最大连续子序列和
  const maxM = maxMiddleL + maxMiddleR;
  // 获得位于数组左半部分的最大连续子序列和
  const maxL = getMax(arr, start, middle);
  // 获得位于数组右半部分的最大连续子序列和
  const maxR = getMax(arr, middle + 1, end);
  // 返回三者最大值
  return Math.max(maxM, maxL, maxR)
};

这种解法的时间复杂度为O(nlgn)

我现在对于分治法的思想理解起来还是由一些困难，感觉数组排序中的归并排序也是利用了分治法的思想

算法还是要加强啊，唉

实现5：动态规划

2019.08.11更新

学习《算法图解》，学习了动态规划的算法，动态规划算法的关键就是将大的问题分解为子问题，使用子问题的答案来解决大问题。

对于连续子串最大和，可以分解为：

1	当前子串的值 = 当前值 + 之前子串的值

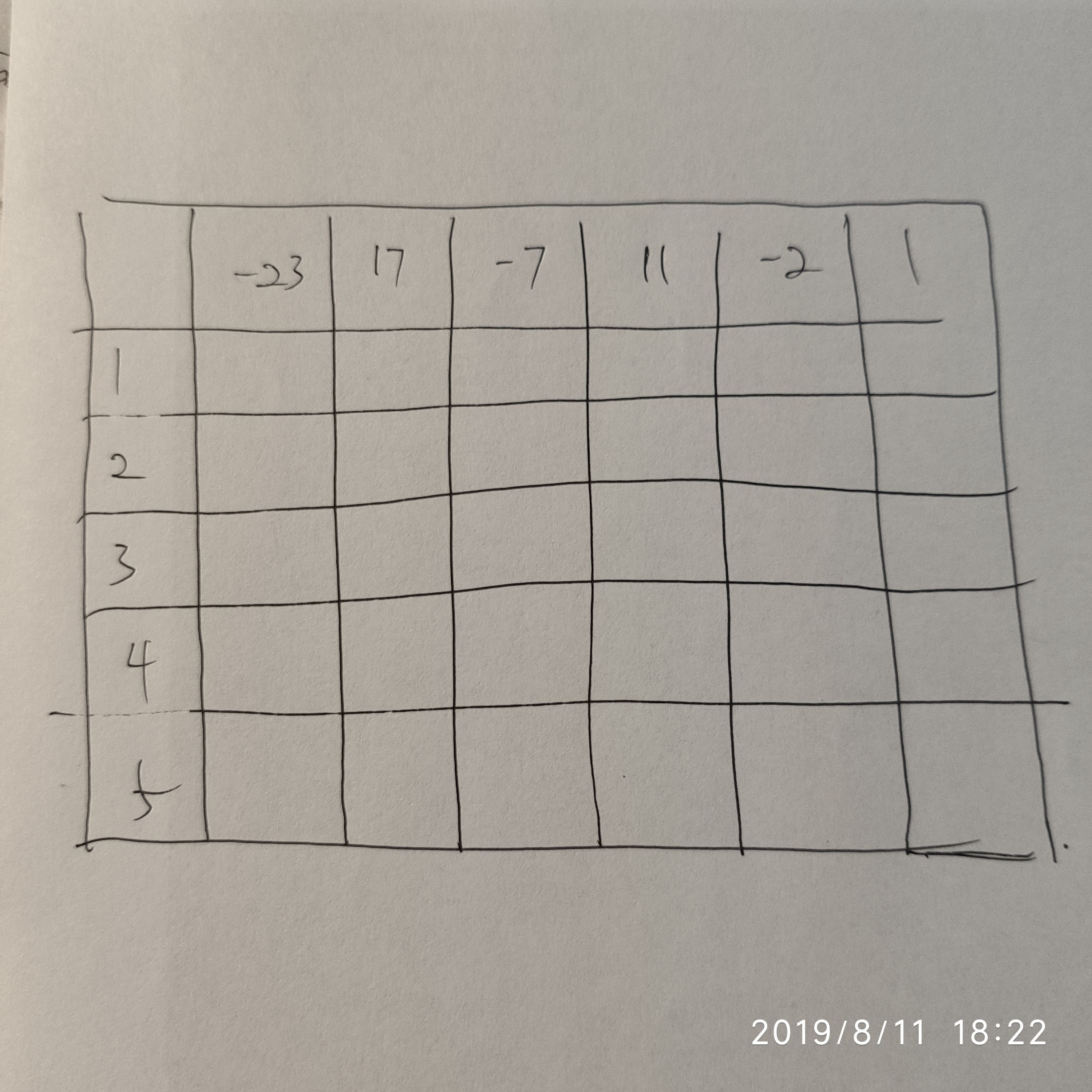
每个动态规划都会涉及一个表格，关键的点就是找到表格的值的计算方法，表格的行坐标是数组的各项的值j，列坐标是子串的长度i，每个单元格的值cell[i][j]就是长度为i的子串，以当前数字结束时，子串的和。

计算第一行的数据，代表的意思就是，当子串长度为1时，子串的值是-23，其他的单元格同理，这样就可以得到这一行的值。并且这一行最大的值就是17

到了第二行，第一个格子是不存在的，因为-23是不能构成长度为2的子串的。实际上表格中分割线以下的位置都是不存在的。

计算下一个格子的时候，就要利用上面的公式，当前值是17，子串长度为2，这个子串的和就等于17加上之前子串的值，之前子串的值就是cell[i-1][j-1]，所以单元格的值就是17 + -23 = -6。，也就是说，长度为2、以17结束的子串即-23, 17这个子串的和是-6。

这样就可以得到这一行的最大值是10，它比17小，所以单元格的最大值仍是17

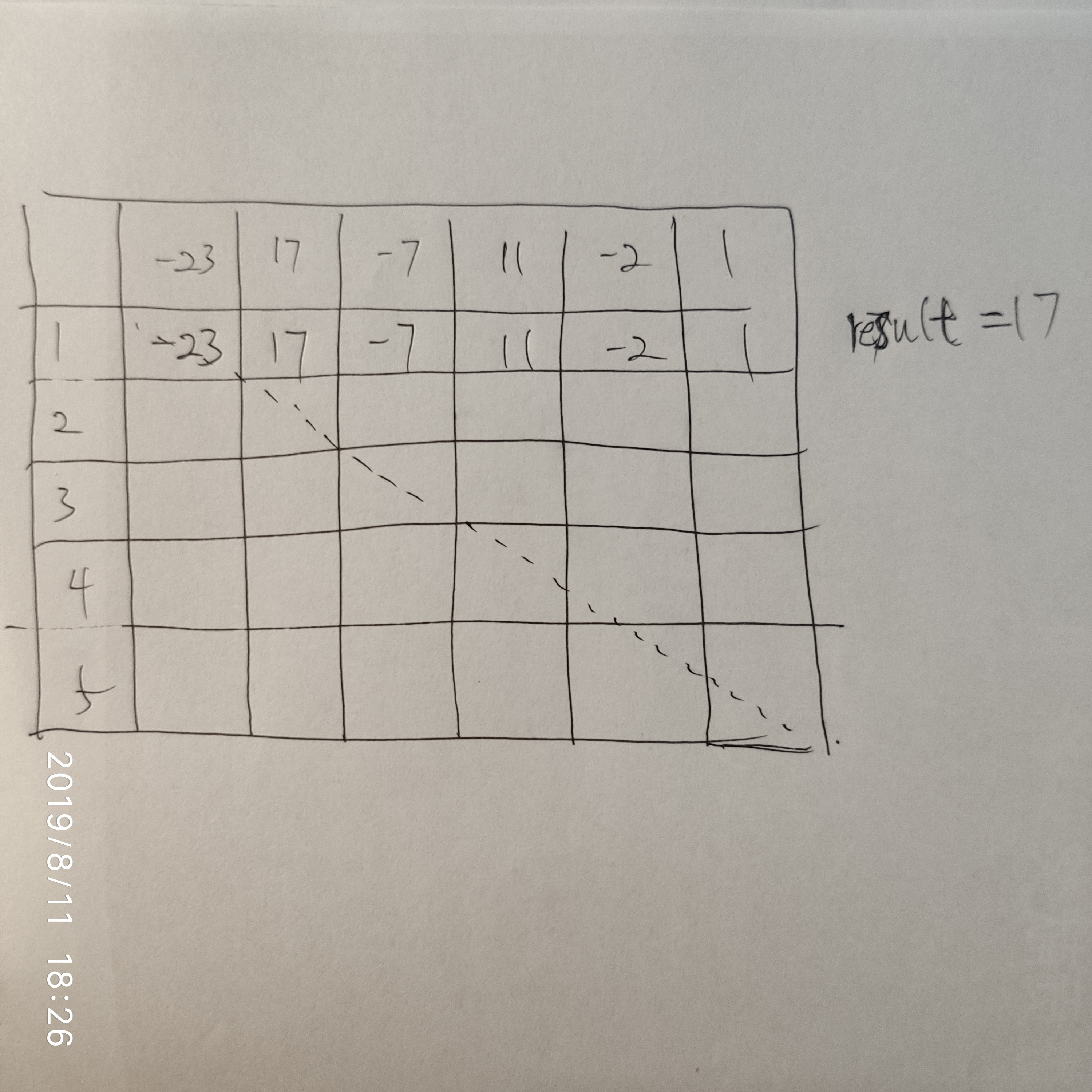
同理可以填完整个表格：

填完之后发现，当前子串的最大值就是21，成员是17, -7, 11

用代码来实现：

// 连续子串最大和
const maxSubSum = arr => {
  let result = 0;
  const cell = [];

  for (let i = 0; i < arr.length; i++) {
    cell[i] = [];
    for (let j = i; j < arr.length; j++) {
      cell[i][j] = arr[j] + ((cell[i-1] && cell[i-1][j-1]) ? cell[i-1][j-1] : 0);
      result = Math.max(result, cell[i][j])
    }
  }

  return result;
};

虽然不一定更简单，但是是有理论依据的思想，有分析问题、建模、代码实现这样一个正确的解决问题的过程。

题目

实现1

实现2

实现3

实现4

实现5：动态规划

参考