算法练习01 数组乱序

发表于 更新于 分类于 阅读次数：

如何将一个数组彻底打乱？。

方法1 使用sort方法

借助sort方法不是真正意义上的完全乱序

1
2
3
4
5
let letters = ['A','B','C','D','E','F','G','H','I','J'];

function shuffle(arr) {
  return [...arr].sort(() = > Math.random() - 0.5)
}

比如A元素大概率出现在数组的头部，J元素大概率出现在数组的尾部，所有元素大概率停留在自己初始位置

原因是：

在Chrome v8引擎源码中，处理sort方法时，使用了插入排序和快排两种方案。当目标数组长度小于10时，使用插入排序；反之，使用快排。

其实不管用什么排序方法，大多数排序算法的时间复杂度介于O(n)到O(n^2)之间，元素之间的比较次数通常情况下要远小于n(n-1)/2，也就意味着有一些元素之间根本就没机会相比较（也就没有了随机交换的可能），这些sort随机排序的算法自然也不能真正随机。

通俗的说，其实我们使用array.sort进行乱序，理想的方案或者说纯乱序的方案是：数组中每两个元素都要进行比较，这个比较有50%的交换位置概率。如此一来，总共比较次数一定为n(n-1)。

而在sort排序算法中，大多数情况都不会满足这样的条件。因而当然不是完全随机的结果了。

某些场景下，这样的方法可以使用。但是这不是真正意义上的完全乱序，一些需求中（比如抽奖）这样的写法会出大问题。

方法2 随机下标

可以采用这样的一种方式，每次随机生成一个下标，将下标对应的数组从原数组中取出来，推入到结果中，如此重复直到原数组为空。

1
2
3
4
5
6
7
8
9
function shuffle(arr) {
  let temp = [...arr];
  let result = [];
  while (temp.length) {
    const index = Math.floor(Math.random() * temp.length);
    result.push(temp.splice(index, 1)[0]);
  }
  return result
}

这种算法用到了splice方法，如果将这个方法的复杂度看看成$O(n)$的话，那么整个程序的复杂度就是$O(n^2)$。

Fisher–Yates shuffle洗牌算法

Fisher–Yates shuffle洗牌算法可以做到理论上的完全乱序，详细过程如下

首先我们有一个已经排好序的数组：

Step1：第一步需要做的就是，从数组末尾开始，选取最后一个元素。

在数组一共 9 个位置中，随机产生一个位置，该位置元素与最后一个元素进行交换

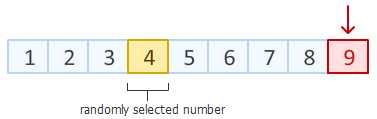
Step2 接下来，对数组倒数第二个元素动手。在除去已经排好的最后一个元素位置以外的8个位置中，随机产生一个位置，该位置元素与倒数第二个元素进行交换。

Step3：理解了前两步骤，接下来就是依次进行，如此简单。

上面这种方式是从后向前进行遍历，我们实现代码：

1
2
3
4
5
6
7
8
9
function shuffle(arr) {
  const copy = [...arr];
  let i = copy.length;
  while (i > 0) {
    const randomIndex = Math.floor(Math.random() * (i--));
    [copy[i], copy[randomIndex]] = [copy[randomIndex], copy[i]];
  }
  return copy;
}

也可以for循环：

1
2
3
4
5
6
7
function shuffle(arr) {
  for (let i = arr.length; i > 0; i--) {
    const randomIndex = Math.floor(Math.random() * i);
    [arr[i], arr[randomIndex]] = [arr[randomIndex], arr[i]];
  }
  return arr;
}

当然也可以从前向后进行遍历：

1
2
3
4
5
6
7
const shuffle = arr => {
  for (let i = 0; i < arr.length; i++) {
    const randomIndex = Math.floor(Math.random() * (arr.length - i)) + i;
    [arr[i], arr[randomIndex]] = [arr[randomIndex], arr[i]]；
  }
  return arr；
};

要注意的是，Math.random的取值范围是[0, 1)，利用Math.random取范围[a, b]的公式是：

1
Math.round(Math.random() * (b - a)) + a

或者：

1
Math.floor(Math.random() * (b - a + 1)) + a

使用Lodash

Lodash的_.shuffle方法也可以做到真正意义的乱序，事实上这个方法正是采用了Fisher–Yates shuffle洗牌算法。

1
2
_.shuffle([1, 2, 3, 4]);
// => [4, 1, 3, 2]

参考